Tovább>>

6. Óra - Arkhimédész törvénye

Arkhimédész törvénye feladatlap>>

Arkhimédész törvénye szerint a folyadékba mártott testekre kétféle erő hat, egyrészt egy lefelé ható ún. nehézségi erő (gravitáció, súly, légnyomás, hidrosztatikai nyomás), másrészt egy felfelé ható ún. felhajtóerő.

Ha a nehézségi erő nagyobb, mint a felhajt erő a folyadékba mártott test lesüllyed.
Ha a két erő kiegyenlíti egymást akkor a test lebeg.
Ha a felhajtóerő nagyobb, mint a nehézségi erő akkor a test úszik.

Archimédész törvénye szerint minden folyadékba vagy gázba merülő testre felhajtóerő hat, amelynek nagysága egyenlő a test által kiszorított folyadék vagy gáz súlyával.

Ez egyébként a gázba merülő testekre is igaz.

PLUSZfeladatok
1. Nézz utána Arkhimédész életének és munkásságának! Pl.: ITT.

KÖVETELMÉNY:
Arkhimédész törvénye
Fogalmak: nehézségi erő, felhajtóerő, süllyedés, lebegés, úszás.

INTERAKTÍV/DIGITÁLIS OKTATÓANYAG:
TTKO - Felhajtóerő, úszás, lebegés, xx 

Arkhimédész kísérlet FILM

Az Arkhimédész sztori

Másik sztori ITT, 9.05-től

7. Óra - Az egyesített gáztörvény

Tk.: 27-33.

A korábbiakban már tanultál arról:

1. milyen összefüggés van a gázok térfogata és hőmérséklete között állandó nyomáson (izobár), Gay-Lussac I. törvénye V1 / T1 = V2 / T2
2. milyen összefüggés van a gázok hőmérséklete és nyomása között állandó térfogaton (izochor) Gay-Lussac II. törvénye p1 / T1 = p2 / T2

A mai órán két újabb állapotváltozásról tanulhatsz.

Gázok állapotváltozása állandó hőmérsékleten (izotermikus)

Hogyan változik a (lezárt) lufiban a levegő nyomása, ha megpróbálod összenyomni?
Hogyan változik a befogott végű, benyomott dugattyújú fecskendőben a nyomás, ha a dugattyút kihúzzuk?

Mindkét esetben állandó volt a hőmérséklet és könnyen belátható, hogy a térfogat csökkentésével (lufi összenyomása) nő a nyomás, míg a térfogat növelésével (fecskendő) a nyomás csökken. A két állapotjelző közti összefüggést Boyle-Mariotte törvénynek nevezzük és az alábbiak szerint írható fel:

p1 x V1 = p2 x V2

Egyesített gáztörvény / gázok általános állapotegyenlete

Végül, vizsgáljuk meg a tanult három állapotjelző (térfogat, nyomás, hőmérséklet) közötti összefüggéseket! Ezt az egyesített gáztörvény írja le, amely az alábbiak szerint írható fel:

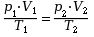
Az egyenlet levezetése megtekinthető ITT.

Az egyenletből megállapítható, hogy

Az összefüggés ténylegesen az ideális gázokra vonatkozik, ezekről korábban már volt szó. Az ideális gázt a valódi gázok elméleti modelljének kell tekintenünk, amelynek haszna, hogy segítségével a valódi gázok az esetek nagy többségében megfelelő pontossággal matematikailag egyszerűen írhatók le.

A gondolatmenetet tovább folytatva végig kellene gondolni, hogyan is fejezhető ki ez az állandó.

A levezetéshez induljunk ki abból, hogy ez egy zárt edényben lévő gáz, melynek nyomása, térfogata és hőmérséklete közt a fenti összefüggés áll fenn. Könnyen beláthatjuk, hogy, ha zárt edényben képzeljük el akkor a gáz tömege is állandó (változatlan), de azt is megtanultad már, hogy az anyagokat nemcsak a tömegükkel, hanem az anyagmennyiségükkel is lehet jellemezni, vagy is állandó anyagmennyiségű (a zárt edényben lévő gáz). Az anyagmennyiség (jele: n) mértékegysége a mól (mol). 1 mol annak a anyagnak az anyagmennyisége, amely 6x1023 db részecskét tartalmaz. Szintén tanultad már, hogy 1 mol normál állapotú gáz (légköri nyomás és 0 Celsius) térfogata 22,41 dm3 = 22414 cm3. Tehát akkor:

p= 101325 Pa (légköri nyomás)
V= 0,022414 m3
T= 273 K

Tudatosítsd az előző mértékegységeket! A nyomás paszkál, a térfogat köbméter, a hőmérséklet Kelvin. Behelyettesítve az alábbi egyenletbe:

101325 x 0,022414 / 273 =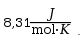

Ez az ún. egyetemes vagy általános gázállandó, jele: R.

Akkor az említett öt adatot kellene egyetlen egyenletben kifejezni: nyomás, térfogat, hőmérséklet, anyagmennyiség, gázállandó. Ez az alábbiak szerint néz ki:

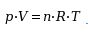
A részletes levezetés megtalálható a Tk. 31. oldalán, valamint ITT.

FELADAT:

KÖVETELMÉNY:
Boyle-Mariotte törvény
Egyesített gáztörvény
Ideális gázok állapotegyenlete
Fogalmak: egyetemes gázállandó, normál állapot

PLUSZfeladat:
Nézz utána Robert Boyle és Edmé Mariotte életének és munkásságának!
 

INTERAKTÍV/DIGITÁLIS OKTATÓANYAG:
Sulinet - Boyle-Mariotte törvény, Robert Boyle élete, munkássága, Edmé Mariotte élete és munkássága, Egyesített gáztörvény, Ideális gázok állapotegyenlete,

Youtube - Boyle-Mariotte törvény 

8. Óra - Számolási feladatok

Gyakorló feladatok a gáztörvényekre

1. Egy hengerben állandó hőmérsékleten gázt sűrítünk össze úgy, hogy térfogata 7 dm³- ről 4 dm³- re csökken, miközben nyomása 1,5*10⁵ Pa lesz. Mennyi volt a gáz kezdeti nyomása?
2. Zárt gázpalackban 27 ⁰C hőmérsékletű 2,4 * 10⁵ Pa nyomású nitrogén van. Mennyi a nitrogén nyomása –13 ⁰C hőmérsékleten?
3. Dugattyúval ellátott hengerben 273 K hőmérsékletű 8 dm³ térfogatú oxigén gáz van. Mekkora lesz az oxigén térfogata, ha állandó nyomáson 120 ⁰C hőmérsékletre melegítjük?
4. Héliummal töltött, nagyon rugalmas meterológiai hőlégballon térfogata 27⁰C hőmérsékleten és 10⁵ Pa nyomáson 1,2 m³. Mekkora lesz a ballon térfogata olyan magasságban, ahol a hélium nyomása 1,2*10⁴Pa, a hőmérséklete pedig -33⁰C?
5. Egy léggömb 12 dm3  levegőt tartalmaz légköri nyomáson, mely körülbelül 100 kPa. Mennyi lenne a léggömb térfogata a tó fenekén, 15 m mélységben?( 10m –ként 100kPa növekedés)
6. Egy levegővel töltött léggömb térfogata 10 dm³  25 °C hőmérsékleten. Egy forró, napos tengerparton a térfogata 10,5 dm³ lesz. Milyen a hőmérséklet a tengerparton? Adja meg az eredményt Celsius fokban és kelvinben. Tételezzük fel, hogy a légköri nyomás állandó!
7. A kén-hexafluorid (SF₆ ) az egyik legsűrűbb ismert gáz. Számítsa ki a gáz sűrűségét 20 °C-on és 100 kPa nyomáson! A számított sűrűség értékeket két tizedesjegy pontossággal adja meg. R= 8,31 J/(K mol). A számításokhoz használja a periódusos rendszerben található atomtömegeket a legközelebbi egész számra kerekítve!
8.  Egy levegőpumpa 1,5 liter, 101,325 kPa nyomású levegőt szív be. A kompresszió után 250 cm³ lesz a levegő térfogata. Milyen nyomás szükséges ehhez, ha hőmérséklet-változással nem kell számolnunk? Add meg a végeredményt Pa, hPa, és atmoszférában!
9. Egy gáz 100 ^oC-on és 100,26 kPa nyomáson 500 cm³ teret tölt be. Mekkora ennek a gáznak a térfogata normál körülmények között?
10. Határozzuk meg, hány részecske van abban az oxigén gázban, amelyiknek nyomása 105Pa, térfogata 1 m³ és hőmérséklete 27 ⁰C?

9. Óra - A gázok állapotváltozásának molekuláris értelmezése, belső energia, hőtan I. főtétele

Tk.: 39-41.

Összegezzük, mi mindent tanultunk idáig a gázokról, illetve egészítsük ki ismereteinket!

A gáz halmazállapotú anyagok kitöltik a rendelkezésre álló teret, állandó ún. rendezetlen hőmozgást végeznek, melynek során ütköznek egymással és az edény falával. Ezt a mozgást Brown-féle mozgásnak is nevezik. A gázrészecskék (atom, molekula) edény falának történő ütközése eredményezi a gáz nyomását. Ez a nyomás annál nagyobb 1. minél nagyobb a rendezetlen hőmozgás sebessége, 2. minél nagyobb az adott térfogatban lévő részecskék száma. Összefüggés fedezhető fel a hőmérséklet és a részecskék sebessége között, minél nagyobb a hőmérséklet annál nagyobb a részecskék átlagos sebessége, ezáltal az adott gáz nyomása.

Az is megállapítható, ha két különböző gázt "összeöntünk" akkor azok spontán elkeverednek, ezt diffúziónak nevezzük. Ez bizonyos folyadékokra is igaz.

Megállapítható:

- állandó hőmérsékleten (izoterm) a térfogat csökkenése a részecske sűrűség növekedését eredményezi, ami növeli a nyomást.
- állandó térfogaton (izochor) a hőmérséklet emelésével a részecskék átlagos sebessége nő, ezáltal a gáz nyomása is növekszik.
- állandó nyomáson (izobár) a térfogat csökkentése a részecskesűrűség növekedését eredményezi, a részecskék gyakrabban ütköznek, ez hőmérséklet emelkedést eredményez.

A nyugalmi állapotban lévő gázrészecskéinek hőmozgását nevezzük a gáz belső energiájának. Ez a belső energia tulajdonképpen a részecskék rendezetlen mozgásából származó mozgási energiák összege. 

A belső energiát a már említett ideális gázokra értelmezzük, amelyek:

- részecskéi pontszerűek,
- részecskéi rendezetlen mozgást végeznek,
- részecskéi egymással és az edény falával rugalmasan ütköznek.

Mivel a gázok belső energiája a részecskék mozgásából adódik, ezért a részecskék mozgásának (átlagos sebességének) növelése a belső energia növekedését eredményezi.

Milyen módszerekkel lehet a részecskék átlagos sebességét növelni? Két lehetőség is kínálkozik:

- a hőmérséklet emelésével, ún. termikus kölcsönhatás
- a térfogat csökkentésével (összenyomás)

A termikus kölcsönhatás során hőt adunk át a rendszernek, pontosan fogalmazva hőmennyiséget (jelölése: Q).
Az összenyomás (mechanikus kölcsönhatás) során pedig munkát végzünk (jelölése: W) a rendszeren.

A folyamatok fordítva is lejátszódhatnak, azaz hőleadás során a gáz belső energiája csökken, míg a belső energia csökkenésekor a gázon végzett munka negatív, azaz a gáz végez munkát.

Az energiamegmaradás törvényét felidézve megállapítható, hogy a gázok belső energiájának változása egyenlő a hőmennyiség és a munkavégzés összegével:

ΔE=Q+W

Ez a hőtan I. főtétele.

KÖVETELMÉNY:
Ideális gázok jellemzői.
Fogalmak: belső energia, Brown-féle mozgás, diffúzió, termikus kölcsönhatás, hőtan I. főtétel.

INTERAKTÍV/DIGITÁLIS OKTATÓANYAG:
Sulinet - A belső energia, A hőtan I. főtétele
x